Bir yazılım ürününün mühendislik, tasarımsal ve mimari niteliklerine baktığımızda erişilebilirlik, ölçeklenebilirlik, hata toleransı, performans, dayanıklılık, güvenlik, emniyet, esneklik, dağıtılabilirlik, test edilebilirlik, çeviklik, kurtarılabilirlik, öğrenilebilirlik, izlenebilirlik..., vb. birçok en iyi hale getirmeye çalıştığı kavram bulunmaktadır. Bunların her birini daha iyi hale getirmek oldukça emek istediği gibi bazıları birbiriyle çelişmektedir. Karar sürecinde bunlardan sebepsizce (makul gerekçeler olmaksızın) sadece bir veya birkaçının ön yargıyla "en önemli" olduğunu düşünmek ürünün toplam kalitesini düşürmektedir. Bu ön yargılardan en sık karşılaştığımız ise performans konusunda oluyor. Bunu iki ekmek almak için bakkala kamyon ile gitmeye benzetebilirsiniz. Bisiklete göre daha hızlı ve taşıma kapasitesi oldukça yüksek olmasına rağmen kullanım senaryosu için saçmadır.
Elbette performansın çok kritik olduğu uygulamalar vardır. Özellikle oyunlarda bunu sık görmekteyiz. Yine aynı oyunlarda performans için diğer kavramların önemi azaltılmak durumundadır. Bu yazıda performans kavramına diğer anlamlarını bir kenara koyup sadece "hız", "tepki süresi" açısından bakacağız.
Algılanan Performans
Diğer tüm performans/hız ölçütlerinden daha önemli olan bence bu kavram. Algılanan hız, kullanıcının uygulamamız hakkındaki ölçüme bağlı olmayan subjektif bir değerdir. Uygulamanın niteliğine ve kullanıcıya göre değişkenlik göstermektedir. Operatörün saniyeler ile yarıştığı, kuyrukta sinirli bir şekilde bekleyen onlarca müşterinin olduğu bir ortamda normalde fark edilmeyecek bir gecikme operatör tarafından haklı olarak "sistem yavaş" tepkilerine yol açabilir. Ya da problem tamamen yanlış kurgulanmış bir arayüz sebebiyle 2 tık ile halledilecek işlemin 10 tıkla yapılması da olabilir. Fakat, çoğu uygulamada kullanıcının hız toleransı gayet yüksektir. Bir tablonun 500ms ya da 50ms'de dolması kullanıcı açısından "anlık" kabul edilecektir. On kat hızlı veri çekmek için ORM, veritabanı, mimari vb. değiştirmeniz kullanıcı açısından hiç fark etmeyecektir (sunucu maliyetleri artar, kullanıcı daha fazla öder diyebilirsiniz ama bir yandan da geliştirme ve bakım maliyetleri de düşeceğinden konu başka yerlere gider). Aynı emek ile yapılacak başka geliştirmelerin toplam faydası çok daha büyük olabilir. Bu konuyla ilgili şu yazıya göz gezdirmenizi tavsiye ederim: https://www.nngroup.com/articles/powers-of-10-time-scales-in-ux/
Asimptotik Analiz
Asimptotik analiz, bir algoritmanın girdi boyutuna verdiği tepkiyi ölçmemizi sağlayan çok güçlü bir araçtır. Örneğin, 100 birim girdi 100 saniyede, 200 birim girdi 200 saniyede hesaplanıyorsa ve bu oran çoğu durumda geçerli ise bu algoritmanın doğrusal bir zaman ilişkisi olduğunu söyleyebiliriz. "Algoritma" dersleri genellikle bu konu ile başlar. Kendisi de özünde ayrık matematiğin bir konusudur ve algoritmalarda kullanımı 1976'da popüler hale gelmiştir. Verilen bir fonksiyonun bir diğer fonksiyon için bir notasyona uygun olup olmadığı ile ilgilenir. Fonksiyonlardan birisi f(x) = 2x+6, diğeri g(x) = x olsun. Big O için ikinci fonksiyona bir çarpan ve sabit eklediğimizde eninde sonunda ilk fonksiyonu geçiyor mu diye bakılır. 3 ile çarpmam veya 2 ile çarpıp 1 eklemem yeterli olacaktır. Fakat, f(x) = x², g(x) = x olduğu durumda ikinci fonksiyonu hangi sayıyla çarpıp ekleme yaparsam yapayım ilk fonksiyon öne geçeceğinden g(x), f(x) için Big O üst sınırı olamaz. Yazılımda bu fonksiyonlardan ilki algoritmanın girdiye göre işlemci üzerinde kaç birim işlem yapacağını öngören T(n) fonksiyonudur. Bu fonksiyonu bir çalışalım:
static void Function(char letter)
{
Console.WriteLine(letter);
}Bu fonksiyonun çalışma süresini sabit zaman (1 birim) olarak kabul ediyoruz. Doğal olarak bu fonksiyon için bulmaya çalıştığımız fonksiyon T(n) = 1 (sabit fonksiyon) olacaktır. Analizi işlemci seviyesine indirgediğimizde, C# kodunun makine koduna dönüşmüş halinde pek tabii çok daha fazla olacaktır. Bunu gözardı edeceğiz, sebebini birazdan açıklayacağım.
Örnekteki fonksiyon için letter parametresinin ne olduğu fark etmeksizin, çalışma süresinde anlamlı bir değişiklik olmayacaktır. Bunu 0'dan sonsuza giden bir grafiğe döktüğümüzde karşılaşacağımız görüntü bir doğru olacaktır.
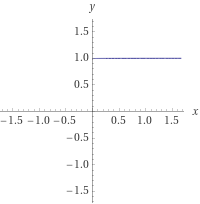
Aynı fonksiyonun her karakteri ekrana tek tek basacak şekle getirilmiş haline bakın:
static void Function(string name)
{
foreach (var character in name){
Console.WriteLine(character);
}
}Bu fonksiyona "cihan" değerini vermemin sonuç açısından aşağıdaki fonksiyondan farkı olmayacaktır:
static void Function(string name)
{
Console.WriteLine(name[0]);
Console.WriteLine(name[1]);
Console.WriteLine(name[2]);
Console.WriteLine(name[3]);
Console.WriteLine(name[4]);
}Bu durumda "cihan" için 5 birim iş yapılırken "abdulmecit" için 10 birim işlem yapılacaktır. Fonksiyonumuz T(n) = n'e dönüşmüş durumda. Ama bundan sonra "x" yerine eleman sayısı için "n" harfini kullanacağız ve fonksiyonun sol kısmını atacağız. T(n) = n yerine sadece n diyeceğiz. Bu durumda grafiğimiz şöyle bir şey olacaktır:
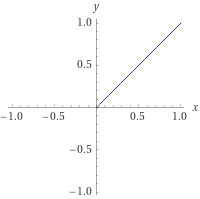
Tabii, gerçek hayatta fonksiyonlarımız koşullar içerir. Kodumuz şu şekilde olsun:
static void Function(string name)
{
if (name.Length % 2 == 0){
Console.WriteLine("A");
return;
}
foreach (var character in name){
Console.WriteLine(character);
}
}Bu durumda uzunluğu tek sayıda olan isimler için daha fazla işlem yapılırken, çift sayıda olanlar için her zaman sabit bir işlem yapılmaktadır. Girdiye göre çalışma zamanı değişmektedir.
Asimptotik analiz için bu kadar bilgi konunun anlaşılması için yeterlidir. Bu bilgilerle şu varsayımları yapabiliyoruz:
- Yapılan analizin çıktısında oluşan polinomun en yüksek kuvvetli değişkenini alıyoruz ve katsayılarından kurtuluyoruz.
Örneğin: 4n² + n + 3 şeklindeki bir analizi doğrudan n² olarak kabul ediyoruz. Zira, girdi boyutunu sonsuza uzattığımızda yüksek olan kuvvetin oluşturduğu eğri her zaman bir noktadan sonra farkı aşmaktadır. Ayrıca düşük kısımlar derleyici, makine ve yazılımcının algoritmayı uygulama biçimine göre değişkenlik gösterir. İşin matematiksel detayı için ayrık matematikte asimptotik notasyon (Big O, Theta, Omega) ve polinom karmaşıklığı konusunu araştırabilirsiniz.
Algoritma analizinde üç temel analiz durumu (case) ve bu durumların performansını ölçmek için kullanılan üç temel notasyon (sınır) vardır. Bu kavramlar sıklıkla karıştırılır.
Analiz Durumları (Cases): Bir algoritmanın belirli bir girdiye göre nasıl davranacağını tanımlar.
- En Kötü Durum (Worst-Case): Algoritmanın çalışabileceği en yavaş senaryo.
- En İyi Durum (Best-Case): Algoritmanın çalışabileceği en hızlı senaryo.
- Ortalama Durum (Average-Case): Tüm olası girdiler düşünüldüğünde beklenen ortalama performans.
Asimptotik Notasyonlar (Sınırlar): Bu durumların matematiksel olarak nasıl büyüdüğünü ifade eder.
Büyük O (Big O): Üst Sınırı (Upper Bound) gösterir. Algoritmanın çalışma zamanının bu fonksiyondan daha hızlı büyüyemeyeceğini garanti eder.
Büyük Omega (Ω): Alt Sınırı (Lower Bound) gösterir. Algoritmanın çalışma zamanının bu fonksiyondan daha yavaş büyüyemeyeceğini garanti eder.
Teta (Θ): Sıkı Sınırı (Tight Bound) gösterir. Algoritmanın büyüme hızı hem üstten (O) hem de alttan (Ω) aynı fonksiyon sınıfıyla sınırlıysa kullanılır. Yani O(n) ve \Omega(n) olan bir şey, \Theta(n)'dir.
Yukarıdaki if'li kod örneğimize bakalım:
En İyi Durum (Best-Case): Girdi uzunluğu çifttir (örn: "ali"). Kod O(1) çalışır.
En Kötü Durum (Worst-Case): Girdi uzunluğu tektir (örn: "cihan"). Kod O(n) çalışır.
Peki, neden Big O genellikle "en kötü durum" şeklinde ele alınır? Çünkü yazılım mühendisliğinde en çok önemsediğimiz şey garantidir. Bir algoritmayı değerlendirirken genellikle "Bu algoritmanın en kötü durumda performansı en fazla ne olur?" (Yani: Worst-Case Big O) sorusunu sorarız. Bu, bize algoritmanın ne kadar kötüleşebileceğinin garantisini verir.
Yazının devamında, "performans" veya "Big O" dediğimizde, sektördeki yaygın kullanımıyla "En Kötü Durum Big O" analizini kestediyorum. Ancak bu iki kavramın teknik olarak farklı olduğunu bilmek çok önemlidir.
Benchmark'lar
Benchmark, bir görevi iki algoritmaya verip saat tutarak hangisinin hızlı çalıştığına karar vermektir. Dikkatsiz yapılan benchmark'lar gereğinden fazla "özel" sonuçlar verebilir. Zira bu ölçüm yönteminde özel olanın yalnızca "girdi" olmasını bekleriz. Fakat, günümüzün işletim sistemlerinde aynı anda birçok uygulama çalışmaktadır. Her uygulama bir diğerinin performansını etkilemektedir. Farklı CPU'larda farklı komut setleri için destekler bulunur, sonuçlar CPU'dan CPU'ya değişebilir. Hava durumu bile sonucu değiştirebilir :). Bu sebeple sonuçlardaki gürültüyü azaltmak için olabildiğince farklı tekrarla farklı makine ve konfigürasyon ile ölçüm yapılması gerekir. Yine de çoğu durumda sonuçlar tabak gibi ortada çıkacağından galibi belirlemek zor olmamaktadır.
.NET tarafında hiçbir kütüphane kullanmadan en kısa yoldan ölçüm yapmak için Stopwatch nesnesini kullanabilirsiniz.
using System.Diagnostics;
List<int> list = new (){ 1, 2, 3, 4, 5 };
HashSet<int> set = new (){ 1, 2, 3, 4, 5 };
Stopwatch stopwatch = new ();
stopwatch.Start();
_ = list.Contains(5);
stopwatch.Stop();
Console.WriteLine(`"List: {stopwatch.ElapsedTicks}");
stopwatch.Restart();
_ = set.Contains(5);
stopwatch.Stop();
Console.WriteLine(`"Set: {stopwatch.ElapsedTicks}");Stopwatch yerine tarih nesneleri veya zamanlayıcı kullanmak pek doğru olmayacaktır. Zira, Stopwatch nesnesi çalışmak için eğer mevcutsa, sistem saati yerine yüksek hassasiyetli donanımsal zamanlayıcı kullanmaktadır.
https://learn.microsoft.com/en-us/dotnet/api/system.diagnostics.stopwatch?view=net-7.0
Fikir vermesi açısından yeterli, fakat bu yöntemi tam teşekküllü bir analiz için kullanmak pek doğru olmayacaktır. Bunun yerine mümkün olduğunca gürültüden ve aşırı değerden arındırılmış sonuçlar veren Benchmark.NET gibi kütüphaneleri kullanabilirsiniz.
Genel-Özel Performans
Bir otomobilin performansını çoğunluğun kullanacağı yollara ve koşullara göre belirliyorsanız burada bir genelleştirme yapıyorsunuzdur. Benzer şekilde bir algoritmanın performansını en sık kullanılacağı durumlara göre genelleştirerek analiz/benchmark yaptığımızda bu genel bir çıkarım sağlayacaktır. Siz offroad meraklısı iseniz genel performansı iyi olan bir araç sizin için anlamlı olmayabilir. Burada da özel kullanıma girmiş oluyoruz. Bir aracın arazi performansının yüksekliğinden dolayı genelde en iyi aracın o olduğunu söylemek nasıl abes ise bir algoritmayı özel bir durumda benchmark'a sokup diğer adaylardan "genelde" daha iyi olduğunu söylemek o kadar abestir.
Bu ayrım basit gözükse de birçok yazıda hatalı çıkarımlar görmek mümkün.
Örneğin, HashSet<T> ve List<T> türünden iki koleksiyonda bir elemanın koleksiyonda olup olmadığının benchmark'ının yapıldığını düşünelim. Her iki koleksiyon için de .Contains metodunu kullanıyor olalım. Sonuçlar aşağıdakine benzer çıkacaktır.
| Method | Mean | Error | StdDev |
|---|---|---|---|
| List | 4.248 ns | 0.0019 ns | 0.0017 ns |
| Hash | 3.369 ns | 0.0018 ns | 0.0015 ns |
İlk hata, bu konunun benchmark gerektirmeyecek seviyede olması. Zira asimptotik analiz yaptığınızda HashSet.Contains için (ortalama ve en kötü durumda) O(1)*, List.Contains için O(n) çıktığını görürsünüz. Bu da genel durumda (girdi boyutu n büyüdükçe) eleman bulma senaryosunda HashSet'in daha iyi olduğunu net bir şekilde gösterir. Analiz sırasında düşük önemdeki kısımları attığımız için küçük girdilerde hassaslığı kaybediyoruz ama bu elle sayılacak kadar bir çoğunluğu ifade ediyor, geriye kalan sonsuz adette kazanan değişmiyor.
(Teknik not: HashSet'in en kötü durumu O(n)'dir, ancak bu çok nadir bir "hash collision" durumudur. Ortalama ve genel kullanımı O(1) kabul edilir.)
İkinci hata ise, bu sonuçlara bakıp "Hash senaryosunun List olandan 1.27 kat daha hızlı olduğu" çıkarımını yapmaktır. Yapılan ölçümde bu koleksiyonların kaç elemanlı olduklarını belirtmedik. Asimptotik analiz girdi arttıkça süredeki değişimi göstermelidir. Yukarıdaki analizi n=2 için yapmıştım. Yani hepsi topu 2 eleman üzerinde arama yapıldı. Bunu 1000 elemana n=1000'e çıkaralım ve sonuçlara tekrar bakalım.
| Method | Mean | Error | StdDev |
|---|---|---|---|
| List1000 | 3.832 ns | 0.0015 ns | 0.0014 ns |
| Hash1000 | 3.298 ns | 0.0052 ns | 0.0046 ns |
Sonuçlar ne kadar da şaşırtıcı değil mi? İki yöntem arasındaki oranın 1.15'e gerilemesini bir yana bırakalım, koleksiyonlar büyüdükleri halde sonuçların bulunma süreleri kısaldı. Ben makineyi değiştirmedim ve görece yakın zamanda ölçüm aldım yine de List için yapılan ölçüm 4.2 ve 3.82 gibi farklı değerler verdi. Bunun sebebi büyük ihtimalle işletim sistemi ile ilgili. Ama diğer bir garip durum aslında List'in asimptotik analize göre daha kötü sonuç vermesi gerekirken bunu yapmıyor olması. Bunun da sebebi çok açık, ben "en iyi" durumu simule ettim. .Contains ile koleksiyondaki ilk elemanı arattım. Bu durumda List tek tek elemanlara bakıp ilkini aldı. En kötü duruma göre (koleksiyonda olmayan bir değer veya son değer) ölçümü 1000 eleman için yeniden yaparsak sonuç şuna benzeyecektir.
| Method | Mean | Error | StdDev |
|---|---|---|---|
| List1000Worst | 141.585 ns | 0.0744 ns | 0.0696 ns |
| Hash1000Worst | 2.574 ns | 0.0007 ns | 0.0006 ns |
Şimdi anlamlı bir fark görüyoruz. Hash'e ne diyorduk "1.27 kat daha hızlı" mı? Şimdi 55 kat daha hızlı. Bir de 100000 eleman ile durumu tekrarlayalım.
| Method | Mean | Error | StdDev |
|---|---|---|---|
| List100_000Worst | 11,606.581 ns | 6.9190 ns | 6.4721 ns |
| Hash100_000Worst | 2.482 ns | 0.0015 ns | 0.0012 ns |
Bizim 55 katımız, 4600 kata çıktı. Öte yandan HashSet kullandığımız yöntemde sonuç değişmedi. List ile olan sonuçlarımızı grafiğe dökecek olursak sonuç şöyle çıkacaktır:
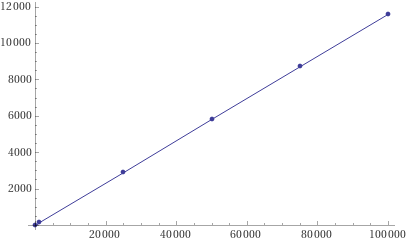
Bu grafik ise tam olarak O(n) (doğrusal) grafiği oluyor. Bu da aslında herhangi bir algoritmanın asimptotik analizini kodun nasıl işlediğini bilmeksizin yaklaşık olarak tahmin edebileceğimiz anlamına geliyor. Buradaki en önemli husus çalıştığınız veri için en iyi ve en kötü senaryoların ne olduğunu bilmekten geçiyor.
Basit sıralama algoritmalarını düşünün, bunlardan Bubble Sort mu yoksa Merge Sort mu daha hızlı diye sorulacak olursa cevabınız ne olurdu? Şayet analizlere bakacak olursak ortalama ve en kötü durum senaryolarında n \log n ile Merge Sort kazanan olacaktır. Bubble Sort ise n² ile kaybedecektir. Fakat, en iyi durum senaryosuna baktığımızda (ki bu, girdinin halihazıra sıralı olmasıdır) optimize edilmiş bir Bubble Sort O(n) ile kazanandır. Eğer yapacağınız iş neredeyse sıralı olan verileri sıralı hale getirmek ise genel geçer hızlı bir algoritma kullanmak yerine bu durumu "en iyi durum" kabul eden algoritmayı seçmelisiniz.
Özetlersek, benchmark sonuçlarına karşı dikkatli olun. Farklı girdi boyutları ile, çok sayıda denenmemiş ölçümlerde "x, y'den n kat daha hızlı" çıkarımlarına güvenmeyin. Girdi boyutu değişse bile, girdinin içeriğine (en iyi durum, en kötü durum) göre algoritmaların farklı davranabileceğini unutmayın.


